Drilling Engineer Average Salary in Somalia 2022
How much money does a Drilling Engineer make in Somalia?
LOW
115,000
SOS AVERAGE
222,000
SOS HIGH
339,000
SOS
A person working as a Drilling Engineer in Somalia typically earns around 222,000 SOS per month. Salaries range from 115,000 SOS (lowest) to 339,000 SOS (highest).
This is the average monthly salary including housing, transport, and other benefits. Drilling Engineer salaries vary drastically based on experience, skills, gender, or location. Below you will find a detailed breakdown based on many different criteria.
Drilling Engineer Salary Distribution in Somalia
The median, the maximum, the minimum, and the range
Salary Range
Drilling Engineer salaries in Somalia range from 115,000 SOS per month (minimum salary) to 339,000 SOS per month (maximum salary).
Median Salary
The median salary is 213,000 SOS per month, which means that half (50%) of people working as Drilling Engineer(s) are earning less than 213,000 SOS while the other half are earning more than 213,000 SOS. The median represents the middle salary value. Generally speaking, you would want to be on the right side of the graph with the group earning more than the median salary.
Percentiles
Closely related to the median are two values: the 25th and the 75th percentiles. Reading from the salary distribution diagram, 25% of Drilling Engineer(s) are earning less than 148,000 SOS while 75% of them are earning more than 148,000 SOS. Also from the diagram, 75% of Drilling Engineer(s) are earning less than 265,000 SOS while 25% are earning more than 265,000 SOS.
What is the difference between the median and the average salary?
Both are indicators. If your salary is higher than both of the average and the median then you are doing very well. If your salary is lower than both, then many people are earning more than you and there is plenty of room for improvement. If your wage is between the average and the median, then things can be a bit complicated. We wrote a guide to explain all about the different scenarios. How to compare your salary
Drilling Engineer Salary Comparison by Years of Experience
How does experience and age affect your pay?
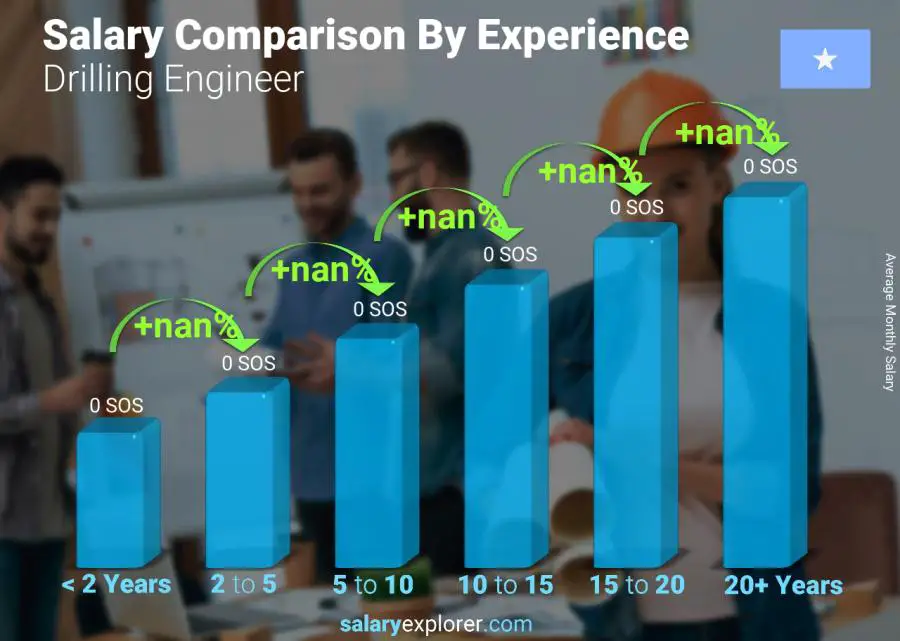
The experience level is the most important factor in determining the salary. Naturally the more years of experience the higher your wage. We broke down Drilling Engineer salaries by experience level and this is what we found.
A Drilling Engineer with less than two years of experience makes approximately 131,000 SOS per month.
While someone with an experience level between two and five years is expected to earn 176,000 SOS per month, 34% more than someone with less than two year's experience.
Moving forward, an experience level between five and ten years lands a salary of 228,000 SOS per month, 30% more than someone with two to five years of experience.
Additionally, Drilling Engineer(s) whose expertise span anywhere between ten and fifteen years get a salary equivalent to 277,000 SOS per month, 21% more than someone with five to ten years of experience.
If the experience level is between fifteen and twenty years, then the expected wage is 302,000 SOS per month, 9% more than someone with ten to fifteen years of experience.
Lastly, employees with more than twenty years of professional experience get a salary of 318,000 SOS per month, 5% more than people with fifteen to twenty years of experience.
Drilling Engineer average salary change by experience in Somalia
| 0 - 2 Years | 131,000 SOS | |
| 2 - 5 Years | +34% | 176,000 SOS |
| 5 - 10 Years | +30% | 228,000 SOS |
| 10 - 15 Years | +21% | 277,000 SOS |
| 15 - 20 Years | +9% | 302,000 SOS |
| 20+ Years | +5% | 318,000 SOS |
Typical Salary Progress for Most Careers
Drilling Engineer Salary Comparison By Education
How do education levels affect salaries?
Displayed below is the average salary difference between different Drilling Engineer(s) who have the same experience but different education levels.
We all know that higher education equals a bigger salary, but how much more money can a degree add to your income? We broke down Drilling Engineer salaries by education level in order to make a comparison.
When the education level is Certificate or Diploma, the average salary of a Drilling Engineer is 156,000 SOS per month.
While someone with a Bachelor's Degree gets a salary of 236,000 SOS per month, 52% more than someone having a Certificate or Diploma degree.
A Master's Degree gets its holder an average salary of 335,000 SOS per month, 42% more than someone with a Bachelor's Degree.
Drilling Engineer average salary difference by education level in Somalia
| Certificate or Diploma | 156,000 SOS | |
| Bachelor's Degree | +52% | 236,000 SOS |
| Master's Degree | +42% | 335,000 SOS |
Is a Master's degree or an MBA worth it? Should you pursue higher education?
A Master's degree program or any post-graduate program in Somalia costs anywhere from 1,300,000 Somali Shilling(s) to 3,890,000 Somali Shilling(s) and lasts approximately two years. That is quite an investment.
You can't really expect any salary increases during the study period, assuming you already have a job. In most cases, a salary review is conducted once education is completed and the degree has been attained.
Many people pursue higher education as a tactic to switch into a higher paying job. The numbers seem to support the thoery. The average increase in compensation while changing jobs is approximately 10% more than the customary salary increment.
If you can afford the costs of higher education, the return on investment is definitely worth it. You should be able to recover the costs in roughly a year or so.
Typical Salary Difference by Education for Most Careers
Drilling Engineer Salary Comparison By Gender
Though gender should not have an effect on pay, in reality, it does. So who gets paid more: men or women? Male Drilling Engineer employees in Somalia earn 13% more than their female counterparts on average.
| Male | 239,000 SOS | |
| Female | -11% | 211,000 SOS |
Salary Comparison By Gender in Somalia for all Careers
Drilling Engineer Average Annual Salary Increment Percentage in Somalia
How much are annual salary increments in Somalia for Drilling Engineer(s)? How often do employees get salary raises?
Drilling Engineer
Drilling Engineer(s) in Somalia are likely to observe a salary increase of approximately 8% every 28 months. The national average annual increment for all professions combined is 5% granted to employees every 28 months.
Somalia / All Professions
The term 'Annual Salary Increase' usually refers to the increase in 12 calendar month period, but because it is rarely that people get their salaries reviewed exactly on the one year mark, it is more meaningful to know the frequency and the rate at the time of the increase.
How to calculate the salary increment percentage?
The annual salary Increase in a calendar year (12 months) can be easily calculated as follows: Annual Salary Increase = Increase Rate x 12 ÷ Increase Frequency
Annual Increment Rate By Industry 2021
| Banking | 2% | |
| Energy | 4% | |
| Information Technology | 6% | |
| Healthcare | 8% | |
| Travel | 1% | |
| Construction | 3% | |
| Education | 5% |
Listed above are the average annual increase rates for each industry in Somalia for the year 2021. Companies within thriving industries tend to provide higher and more frequent raises. Exceptions do exist, but generally speaking, the situation of any company is closely related to the economic situation in the country or region. These figures tend to change frequently.
Worldwide Salary Raises: All Countries and All Jobs
Drilling Engineer Bonus and Incentive Rates in Somalia
How much and how often are bonuses being awarded?
Share This Chart Tweet Get Chart Linkhttp://www.salaryexplorer.com/charts/somalia/engineering/drilling-engineer/annual-salary-bonus-rate-somalia-drilling-engineer.jpg
A Drilling Engineer is considered to be a low bonus-based job due to the generally limited involvement in direct revenue generation, with exceptions of course. The people who get the highest bonuses are usually somehow involved in the revenue generation cycle.
90% of surveyed staff reported that they haven't received any bonuses or incentives in the previous year while 10% said that they received at least one form of monetary bonus.
Those who got bonuses reported rates ranging from 1% to 3% of their annual salary.
| Received Bonus | 10% | |
| No Bonus | 90% |
Types of Bonuses Considered
Individual Performance-Based BonusesThe most standard form of bonus where the employee is awarded based on their exceptional performance.
Company Performance BonusesOccasionally, some companies like to celebrate excess earnings and profits with their staff collectively in the form of bonuses that are granted to everyone. The amount of the bonus will probably be different from person to person depending on their role within the organization.
Goal-Based BonusesGranted upon achieving an important goal or milestone.
Holiday / End of Year BonusesThese types of bonuses are given without a reason and usually resemble an appreciation token.
Bonuses Are Not Commissions!
People tend to confuse bonuses with commissions. A commission is a prefixed rate at which someone gets paid for items sold or deals completed while a bonus is in most cases arbitrary and unplanned.
What makes a position worthy of good bonuses and a high salary?
The main two types of jobs | |
| Revenue Generators | Supporting Cast |
Employees that are directly involved in generating revenue or profit for the organization. Their field of expertise usually matches the type of business. | Employees that support and facilitate the work of revenue generators. Their expertise is usually different from that of the core business operations. |
Example: | Example: |
Revenue generators usually get more and higher bonuses, higher salaries, and more frequent salary increments. The reason is quite simple: it is easier to quantify your value to the company in monetary terms when you participate in revenue generation.
Bonus Comparison by Seniority Level
Top management personnel and senior employees naturally exhibit higher bonus rates and frequencies than juniors. This is very predictable due to the inherent responsibilities of being higher in the hierarchy. People in top positions can easily get double or triple bonus rates than employees down the pyramid.
Drilling Engineer Average Hourly Wage in Somalia
1,280 SOS per hourThe average hourly wage (pay per hour) in Somalia is 1,280 SOS. This means that the average Drilling Engineer in Somalia earns approximately 1,280 SOS for every worked hour.
The hourly wage is the salary paid in one worked hour. Usually jobs are classified into two categories: salaried jobs and hourly jobs. Salaried jobs pay a fix amount regardless of the hours worked. Hourly jobs pay per worked hour. To convert salary into hourly wage the above formula is used (assuming 5 working days in a week and 8 working hours per day which is the standard for most jobs). The hourly wage calculation may differ slightly depending on the worked hours per week and the annual vacation allowance. The figures mentioned above are good approximations and are considered to be the standard. One major difference between salaried employees and hourly paid employees is overtime eligibility. Salaried employees are usually exempt from overtime as opposed to hourly paid staff.
Drilling Engineer VS Other Jobs
The average salary for Drilling Engineer is 1% more than that of Engineering. Also, Engineering salaries are 16% less than those of All Jobs.
Salary comparison with similar jobs
| Job Title | Average Salary |
| Acoustics Engineer | 218,000 SOS |  -2% |
| Assembly Engineering Technician | 176,000 SOS | -21% |
| Assistant Chief Engineer | 255,000 SOS |  +15% |
| Associate Engineer | 204,000 SOS | -8% |
| Autocad Operator | 143,000 SOS | -36% |
| Automation Engineer | 243,000 SOS | +10% |
| Avionic System Support Engineer | 216,000 SOS | -3% |
| Biochemical Engineer | 212,000 SOS | -4% |
| BMS Engineer | 212,000 SOS | -4% |
| Bridge and Lock Tender | 123,000 SOS | -45% |
| Broadcast Engineer | 224,000 SOS | +1% |
| CAD Design Engineer | 235,000 SOS | +6% |
| CAD Designer | 143,000 SOS | -36% |
| CAE Engineer | 224,000 SOS | +1% |
| Ceramics Engineer | 208,000 SOS | -6% |
| Civil Engineer | 235,000 SOS | +6% |
| Commissioning Engineer | 222,000 SOS | +0% |
| Communications Engineer | 247,000 SOS | +11% |
| Condition Monitoring Engineer | 197,000 SOS | -11% |
| Contract Associate Engineer | 216,000 SOS | -3% |
| Control Systems Engineer | 224,000 SOS | +1% |
| Controls Engineer | 224,000 SOS | +1% |
| Controls Software Engineer | 201,000 SOS | -9% |
| Corrosion Engineer | 208,000 SOS | -6% |
| Design Engineer | 233,000 SOS | +5% |
| Drafter | 143,000 SOS | -36% |
| Drafting Manager | 262,000 SOS | +18% |
| Drilling Engineer | 222,000 SOS | +0% |
| Electrical Draughtsman | 116,000 SOS | -48% |
| Electrical Engineer | 251,000 SOS | +13% |
| Electrical Engineering Manager | 328,000 SOS | +48% |
| Electromechanical Engineering Technologist | 245,000 SOS | +10% |
| Electromechanical Equipment Assembler | 120,000 SOS | -46% |
| Energy Engineer | 239,000 SOS | +8% |
| Engine Assembler | 102,000 SOS | -54% |
| Engineer | 241,000 SOS | +9% |
| Engineering Account Manager | 260,000 SOS | +17% |
| Engineering Chief Designer | 258,000 SOS | +16% |
| Engineering Consultant | 309,000 SOS | +39% |
| Engineering Key Account Manager | 328,000 SOS | +48% |
| Engineering Lab Technician | 216,000 SOS | -3% |
| Engineering Planning Manager | 318,000 SOS | +43% |
| Engineering Production Manager | 405,000 SOS | +83% |
| Engineering Project Analyst | 266,000 SOS | +20% |
| Engineering Project Coordinator | 264,000 SOS | +19% |
| Engineering Project Director | 463,000 SOS | +110% |
| Engineering Project Manager | 320,000 SOS | +44% |
| Engineering Research and Development Manager | 366,000 SOS | +65% |
| Engineering Safety Coordinator | 177,000 SOS | -20% |
| Engineering Sales Manager | 312,000 SOS | +41% |
| Engineering Technician | 177,000 SOS | -20% |
| Engineering Technologist | 177,000 SOS | -20% |
| Environmental Engineer | 224,000 SOS | +1% |
| Equipment Engineer | 208,000 SOS | -6% |
| Equipment Engineering Manager | 301,000 SOS | +36% |
| Estimator | 197,000 SOS | -11% |
| Fabrication Specialist | 162,000 SOS | -27% |
| Fabricator | 104,000 SOS | -53% |
| Facade Engineer | 222,000 SOS | +0% |
| Fiber Analyst | 131,000 SOS | -41% |
| Field Engineer | 237,000 SOS | +7% |
| Field Engineering Manager | 386,000 SOS | +74% |
| Fire Engineer | 230,000 SOS | +4% |
| Fitter and Turner | 73,300 SOS | -67% |
| Forestry Strategic Planner | 266,000 SOS | +20% |
| Generation Engineer | 231,000 SOS | +4% |
| Genetic Engineer | 251,000 SOS | +13% |
| Geological Engineer | 235,000 SOS | +6% |
| Geotechnical Engineer | 243,000 SOS | +10% |
| Heavy Equipment Mechanic | 122,000 SOS | -45% |
| Highway Engineer | 228,000 SOS | +3% |
| HSE Professional | 212,000 SOS | -4% |
| HVAC Engineer | 243,000 SOS | +10% |
| HVAC Supervisor | 208,000 SOS | -6% |
| Industrial Engineer | 220,000 SOS | -1% |
| Industrial Engineering Technologist | 220,000 SOS | -1% |
| Instrument Engineer | 226,000 SOS | +2% |
| Instrumentation and Control Engineer | 226,000 SOS | +2% |
| Instrumentation Engineer | 226,000 SOS | +2% |
| Instrumentation Manager | 226,000 SOS | +2% |
| Irrigation Engineer | 222,000 SOS | +0% |
| Licensed Aircraft Engineer | 245,000 SOS | +10% |
| Locomotive Engineer | 220,000 SOS | -1% |
| Maintenance Engineer | 214,000 SOS | -4% |
| Maintenance Fitter | 81,000 SOS | -63% |
| Maintenance Manager | 228,000 SOS | +3% |
| Manufacturing Engineer | 220,000 SOS | -1% |
| Marine Engineer | 230,000 SOS | +4% |
| Materials Engineer | 224,000 SOS | +1% |
| Materials Researcher | 212,000 SOS | -4% |
| Materials Technician | 166,000 SOS | -25% |
| Mechanical and Electrical Engineer | 245,000 SOS | +10% |
| Mechanical Design Engineer | 243,000 SOS | +10% |
| Mechanical Designer | 197,000 SOS | -11% |
| Mechanical Engineer | 243,000 SOS | +10% |
| Mechanical Engineering Manager | 320,000 SOS | +44% |
| Mechanical Inspector | 220,000 SOS | -1% |
| Mechatronics Engineer | 243,000 SOS | +10% |
| Mining Engineer | 228,000 SOS | +3% |
| Oil and Petrochemical Engineer | 249,000 SOS | +12% |
| Optical Engineer | 222,000 SOS | +0% |
| Optical Instrument Assembler | 116,000 SOS | -48% |
| PCB Assembler | 82,900 SOS | -63% |
| Photonics Engineer | 251,000 SOS | +13% |
| Photonics Technician | 204,000 SOS | -8% |
| Pipeline Engineer | 208,000 SOS | -6% |
| Piping Designer | 123,000 SOS | -45% |
| Piping Engineer | 208,000 SOS | -6% |
| Planning Engineer | 231,000 SOS | +4% |
| Pressure Vessel Inspector | 108,000 SOS | -51% |
| Principal Cost Engineer | 231,000 SOS | +4% |
| Principal Engineer | 231,000 SOS | +4% |
| Principal Support Engineer | 231,000 SOS | +4% |
| Process Engineer | 226,000 SOS | +2% |
| Process Operator | 135,000 SOS | -39% |
| Product Development Engineer | 237,000 SOS | +7% |
| Product Development Technician | 166,000 SOS | -25% |
| Product Engineer | 237,000 SOS | +7% |
| Product Safety Engineer | 216,000 SOS | -3% |
| Production Engineer | 228,000 SOS | +3% |
| Project Engineer | 241,000 SOS | +9% |
| Proposal Manager | 295,000 SOS | +33% |
| Purchasing Engineer | 210,000 SOS | -5% |
| Quality Assurance Engineer | 226,000 SOS | +2% |
| Rail Engineer | 230,000 SOS | +4% |
| Robotics Engineer | 258,000 SOS | +16% |
| Robotics Technician | 187,000 SOS | -16% |
| Safety Engineer | 228,000 SOS | +3% |
| Safety Inspector | 177,000 SOS | -20% |
| Safety Manager | 270,000 SOS | +22% |
| Safety Officer | 120,000 SOS | -46% |
| Sales Engineer | 243,000 SOS | +10% |
| Scheduling Engineer | 208,000 SOS | -6% |
| Service Engineer | 239,000 SOS | +8% |
| Solar Engineer | 247,000 SOS | +11% |
| Staff Engineer | 226,000 SOS | +2% |
| Static Equipment Engineer | 222,000 SOS | +0% |
| Stationary Engineer | 206,000 SOS | -7% |
| Stress Engineer | 212,000 SOS | -4% |
| Structural Analysis Engineer | 224,000 SOS | +1% |
| Structural Designer | 201,000 SOS | -9% |
| Structural Engineer | 224,000 SOS | +1% |
| Structural Technician | 147,000 SOS | -34% |
| Supply Chain Specialist | 224,000 SOS | +1% |
| Surveyor | 172,000 SOS | -22% |
| Technical Affairs Officer | 116,000 SOS | -48% |
| Technical Assistant | 116,000 SOS | -48% |
| Technical Engineer | 197,000 SOS | -11% |
| Technical Support Engineer | 197,000 SOS | -11% |
| Tender Engineer | 204,000 SOS | -8% |
| Test Development Engineer | 224,000 SOS | +1% |
| Transportation Engineer | 216,000 SOS | -3% |
| Validation Engineer | 204,000 SOS | -8% |
| Verification Engineer | 216,000 SOS | -3% |
| Wastewater Engineer | 224,000 SOS | +1% |
| Wind Energy Engineer | 231,000 SOS | +4% |
| Wind Energy Operations Manager | 303,000 SOS | +37% |
| Work Planner | 160,000 SOS | -28% |
Government vs Private Sector Salary Comparison
Where can you get paid more, working for a private company or for the government? Public sector employees in Somalia earn 18% more than their private sector counterparts on average across all sectors.
| Private Sector | 233,000 SOS | |
| Public Sector | +18% | 275,000 SOS |
